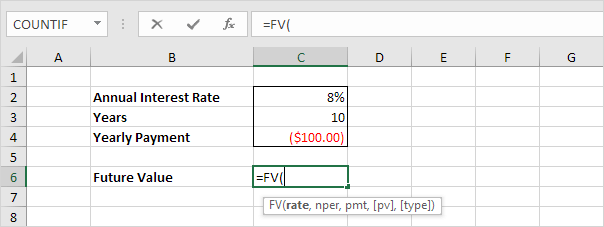
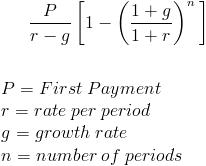Pv Of Growing Annuity Excel Formula

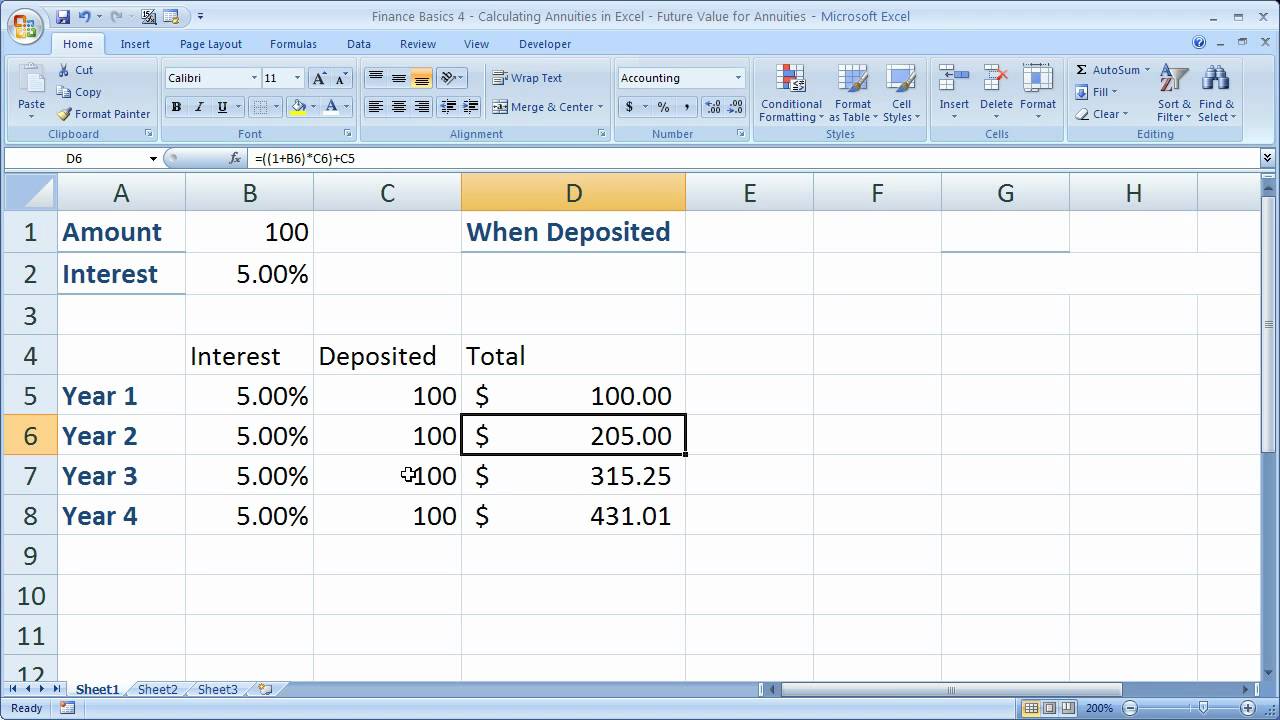
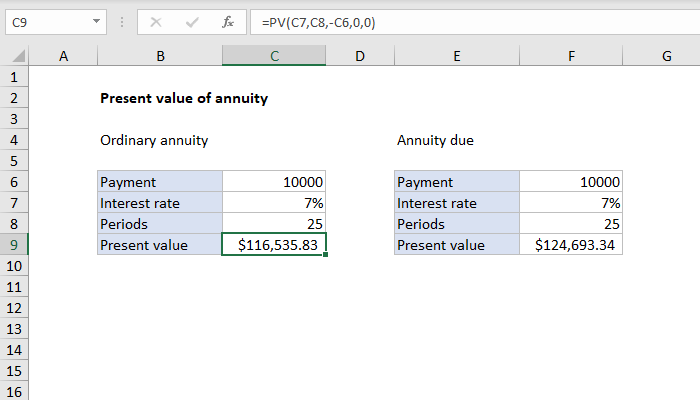
In the example shown the formula in c9 is.

Pv of growing annuity excel formula. Present value of a growing annuity formula example. Excel can be an extremely useful tool for these calculations. The excel present value of a growing annuity calculator available for download below is used to compute the present value by entering details relating to the regular payment growth rate discount. Pv pmt x 1 1 g n x 1 i n i g instructions.

Annuity cash flows grow at 0 i e they are constant while graduated annuity cash flows grow at. The calculator uses the present value of a growing annuity formula as shown below. It differs from ordinary annuity and annuity due in that the periodic cash flows in a growing annuity grow at a constant rate but stays constant in an annuity. A growing annuity is an annuity where the payments grow at a particular rate.

Excel can perform complex calculations and has several formulas for just about any role within finance and banking including unique annuity calculations that use present and future value of annuity formulas. A growing annuity is a finite stream of equal cash flows that occur after equal interval of time and grow at a constant rate. A growing annuity can also be known as an increasing or graduated annuity. Calculating the present value of an annuity using microsoft excel is a fairly straightforward exercise as long as you know a given annuity s interest rate payment amount and duration but it s.

The basic annuity formula in excel for present value is pv rate nper pmt. So the two types of cash flows differ only in the growth rate of the cash flows. Pv c5 c6 c4 0 0 explanation an annuity is a series of equal cash flows spaced equally in time. However a graduated annuity is one in which the cash flows are not all the same instead they are growing at a constant rate.

Pv pmt x 1 1. Strictly speaking an annuity is a series of equal cash flows equally spaced in time. The growing annuity payment from present value formula shown above is used to calculate the initial payment of a series of periodic payments that grow at a proportionate rate. The payments are made at the end of each period for a fixed number of periods a discount rate is applied and the formula discounts the value of each payment back to the original value at the start of the first period the present value.

The formula for the present value of a growing annuity can be written as this formula is the general formula for summing the discounted future cash flows along with using 1 g to factor in that each future cash flow will increase at a specific rate. If a payment of 8 000 is received at the end of period 1 and grows at a rate of 3 for each subsequent period for a total of 10 periods and the discount rate is 6 then the value of the payments today is given by the present value of a growing annuity formula as follows.